El algoritmo de Euclides sirve para obtener el máximo común divisor de dos números enteros positivos. Y con el resultado se podrá hallar el mínimo común múltiplo (M.C.M.).
Máximo Común Divisor
El máximo común divisor de dos números enteros positivos a y b es otro número entero positivo c tal que si dividimos a/c y b/c, los restos de las divisiones son 0, y además no existe otro número mayor que c que tenga esta caracterísitica. Como nos decían en el "cole", el máximo común dívisor (mcd) de dos enteros a y b es el mayor entero c que divide exactamente a a y b.
Aunque en el colegio nos enseñan a encontrar el mcd a partir de la descomposición en factores primos de a y b, esa no es una buena forma de obtener el mcd computacionalmente, ya que el algoritmo para descomponer en factores primos es muy costoso, en términos de computación. El algoritmo de Euclides es bastante más eficiente para obtener el mcd, aunque normalmente sorprende un poco cuando tenemos contacto con él por primera vez.
El algoritmo de Euclides es el siguiente.
Algoritmo de EuclidesSiendo a y b dos enteros positivos tales que a>b, comenzamos dividiendo a/b, con lo que obtendremos un resto r1 y un cociente q1. Hacemos la operación q1=a/b, utilizando la división entera, sin decimales.... pero realmente no sólo nos interesa el resultado o cociente de la división, sino que nos interesa también el resto, así que la operación la vamos a reescribir de otra forma.
Es importante que llamemos "a" al mayor de los dos números. Debemos dividir a entre b y obtener un cociente (al que llamaremos q1) y un resto (al que llamaremos r1).
A partir de esa primera división, es necesario repetir un proceso:
Siguiendo con el ejemplo, en la segunda iteración, dividiríamos b/r1 obteniendo un resto r2 (hacemos la operación de división para obtener el cociente, al que llamamos q2 y la de obtener el resto, al que llamamos r2), de tal manera que se cumpla lo siguiente:
al que llamamos r2), de tal manera que se cumpla lo siguiente:
Como comentábamos al principio, es muy sencillo implementarlo iterativamente. Basta tener en cuenta que en cada vuelta del bucle, y siempre a partir de la segunda iteración hay que hacer que el divisor sea el resto de la iteración anterior y el dividendo sea el divisor de la iteración anterior.
Observa este código en C#.
En él vamos a utilizar dos variables enteras i1 e i2, que inicialmente van a contener los valores de los dos enteros a y b que se pasen como parámetros, de tal manera que i1 tendrá al mayor de los dos, e i2 al más pequeño... y a partir de ahí nos metemos en un bucle. La dinámica es siempre la misma: obtenemos el resto de la división, y si no es 0, debemos hacer otra repetición. Pero antes de la siguiente repetición, desplazamos los valores: lo que contenía i1 ya no nos sirve. Metemos en i1 lo que tiene i2, y en i2 el resto que hemos obtenido....
Al principio cuesta un poco de coger... te recomiendo hacer una traza mentalmente (o mejor, ayudándote de papel).
Te darás cuenta de cómo se van "desplazando los valores" a medida que vamos dividiendo hasta obtener el resto 0... aunque, realmente... no estamos utilizando los cocientes, sino sólo los restos ;-)
Aunque en la introducción hemos mencionado la división ("/"), realmente no es del todo cierto... sólo queremos los restos, no el cociente...(operador módulo o resto: "%" en C#). Hemos introducido esta pequeña mentira en la explicación (pero no en el código) porque cuando dividimos "a mano", realmente en la misma operación de división obtenemos dos resultados a la vez: por un lado el cociente y por otro, el resto. Sin embargo, los lenguajes de programación hacen cada una de esas cosas por separado: pueden obtener un cociente sin necesidad de obtener un resto y al revés, obtener un resto sin necesidad de dividir... así que en nuestro algoritmo no dividimos realmente: sólo obtenemos el resto. Si lo hiciéramos "a mano", tendríamos que dividir, con lo que obtendríamos el cociente y el resto simultáneamente, pero despreciaríamos el cociente y nos quedaríamos sólo con el resto.
Muy relacionado con el máximo común divisor está el mínimo común múltiplo (mcm).
El mcm de dos enteros positivos a y b es un valor c entero y positivo tal que al dividir c/a y c/b el resto es 0, y además no existe otro número menor que c que cumpla esta condición.
Hay una relación muy sencilla entre mcm y mcd. Es ésta:
Así pues, también podemos obtener el mcm mediante el algoritmo de Euclides.
NOTA: Observa que primero se divide a entre el mcd, en lugar de multiplicar a*b. Esto se hace para evitar un posible desbordamiento al multiplicar a*b.
En general, los algoritmos 1 y 2 no son muy apropiados para implementarse directamente en un lenguaje de programación, especialmente porque consumen mucha memoria. Si no se necesitan los valores intermedios, y sólo se desea calcular el máximo común divisor de dos números enteros, conviene usar estas variantes:
Algoritmo de Euclides tradicional implementado de manera recurrente
Algoritmo de Euclides tradicional implementado de manera iterativa
Algoritmo de Euclides extendido implementado de manera recurrente
Algoritmo de Euclides extendido implementado de manera iterativa
Algoritmo de Euclides extendido implementado de manera iterativa con matrices
Acerca de la notación empleada:
Texto literal y prueba: http://latecladeescape.com/con-nombre-propio/algoritmo-de-euclides-mcd-y-mcm.html
Resumen: http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
Máximo Común Divisor
El máximo común divisor de dos números enteros positivos a y b es otro número entero positivo c tal que si dividimos a/c y b/c, los restos de las divisiones son 0, y además no existe otro número mayor que c que tenga esta caracterísitica. Como nos decían en el "cole", el máximo común dívisor (mcd) de dos enteros a y b es el mayor entero c que divide exactamente a a y b.Aunque en el colegio nos enseñan a encontrar el mcd a partir de la descomposición en factores primos de a y b, esa no es una buena forma de obtener el mcd computacionalmente, ya que el algoritmo para descomponer en factores primos es muy costoso, en términos de computación. El algoritmo de Euclides es bastante más eficiente para obtener el mcd, aunque normalmente sorprende un poco cuando tenemos contacto con él por primera vez.
El algoritmo de Euclides es el siguiente.
Algoritmo de EuclidesSiendo a y b dos enteros positivos tales que a>b, comenzamos dividiendo a/b, con lo que obtendremos un resto r1 y un cociente q1. Hacemos la operación q1=a/b, utilizando la división entera, sin decimales.... pero realmente no sólo nos interesa el resultado o cociente de la división, sino que nos interesa también el resto, así que la operación la vamos a reescribir de otra forma.
Es importante que llamemos "a" al mayor de los dos números. Debemos dividir a entre b y obtener un cociente (al que llamaremos q1) y un resto (al que llamaremos r1).
a=q1·b+r1
Los lenguajes de programación suelen tener un operador para efectuar la división entera (con lo que obtendremos q1. Por ejemplo, en C#: "q1=a/b;"), y otro para obtener el resto o módulo de la división (con lo que obtendremos r1. Por ejemplo, en C#: "r1=a%b;").A partir de esa primera división, es necesario repetir un proceso:
- dividir el dividendo del paso anterior entre el resto del paso anterior
- despreciar el cociente
- si el resto es 0, el mcd es el divisor de esta operacion, es decir, el último resto no nulo (recordemos que el divisor de esta operación fué el resto en la anterior.
- Si el resto no es 0, ir al primer paso
Siguiendo con el ejemplo, en la segunda iteración, dividiríamos b/r1 obteniendo un resto r2 (hacemos la operación de división para obtener el cociente, al que llamamos q2 y la de obtener el resto,
 al que llamamos r2), de tal manera que se cumpla lo siguiente:
al que llamamos r2), de tal manera que se cumpla lo siguiente:b=q2·r1+r2
En la tercera iteración, dividimos r1/r2 obteniendo un resto r3r1=q3·r2+r3
Y se continúa así hasta obtener un resto 0. El último resto rk distinto de cero es el mcd.rk-2=qk·rk-1+rk
rk-1=qk+1·rk+0
rk-1=qk+1·rk+0
rk es el mcd(a,b)
Es decir, empezamos dividiendo un número entre otro (obteniendo el resto también, no sólo el cociente), y a partir de ahí, seguimos dividiendo el número más pequeño entre el resto que nos ha salido... y continuamos dividiendo por el resto anterior una vez y otra hasta que en ese proceso repetitivo obtengamos un resto que sea 0. ¡Ya lo tenemos!. El mcd es es resto anterior (que no es cero). Como comentábamos al principio, es muy sencillo implementarlo iterativamente. Basta tener en cuenta que en cada vuelta del bucle, y siempre a partir de la segunda iteración hay que hacer que el divisor sea el resto de la iteración anterior y el dividendo sea el divisor de la iteración anterior.
Observa este código en C#.
En él vamos a utilizar dos variables enteras i1 e i2, que inicialmente van a contener los valores de los dos enteros a y b que se pasen como parámetros, de tal manera que i1 tendrá al mayor de los dos, e i2 al más pequeño... y a partir de ahí nos metemos en un bucle. La dinámica es siempre la misma: obtenemos el resto de la división, y si no es 0, debemos hacer otra repetición. Pero antes de la siguiente repetición, desplazamos los valores: lo que contenía i1 ya no nos sirve. Metemos en i1 lo que tiene i2, y en i2 el resto que hemos obtenido....
static int EuclidesMCD(int a, int b) { int iaux; //auxiliar a = Math.Abs(a); //tomamos valor absoluto b = Math.Abs(b); int i1=Math.Max(a,b); //i1 = el más grande int i2=Math.Min(a,b); //i2 = el más pequeño do { iaux = i2; //guardar divisor i2 = i1 % i2; //resto pasa a divisor i1 = iaux; //divisor pasa a dividendo } while (i2 != 0); return i1; //ultimo resto no nulo }
Al principio cuesta un poco de coger... te recomiendo hacer una traza mentalmente (o mejor, ayudándote de papel).
Te darás cuenta de cómo se van "desplazando los valores" a medida que vamos dividiendo hasta obtener el resto 0... aunque, realmente... no estamos utilizando los cocientes, sino sólo los restos ;-)
Aunque en la introducción hemos mencionado la división ("/"), realmente no es del todo cierto... sólo queremos los restos, no el cociente...(operador módulo o resto: "%" en C#). Hemos introducido esta pequeña mentira en la explicación (pero no en el código) porque cuando dividimos "a mano", realmente en la misma operación de división obtenemos dos resultados a la vez: por un lado el cociente y por otro, el resto. Sin embargo, los lenguajes de programación hacen cada una de esas cosas por separado: pueden obtener un cociente sin necesidad de obtener un resto y al revés, obtener un resto sin necesidad de dividir... así que en nuestro algoritmo no dividimos realmente: sólo obtenemos el resto. Si lo hiciéramos "a mano", tendríamos que dividir, con lo que obtendríamos el cociente y el resto simultáneamente, pero despreciaríamos el cociente y nos quedaríamos sólo con el resto.
Mínimo Común Múltiplo.
Muy relacionado con el máximo común divisor está el mínimo común múltiplo (mcm).
El mcm de dos enteros positivos a y b es un valor c entero y positivo tal que al dividir c/a y c/b el resto es 0, y además no existe otro número menor que c que cumpla esta condición.
Hay una relación muy sencilla entre mcm y mcd. Es ésta:
mcm(a,b)=(a·b)/mcd(a,b)
Así pues, también podemos obtener el mcm mediante el algoritmo de Euclides.
static int EuclidesMCM(int a, int b) { return (a / EuclidesMCD(a, b)) * b; }
NOTA: Observa que primero se divide a entre el mcd, en lugar de multiplicar a*b. Esto se hace para evitar un posible desbordamiento al multiplicar a*b.
EN RESUMEN
En general, los algoritmos 1 y 2 no son muy apropiados para implementarse directamente en un lenguaje de programación, especialmente porque consumen mucha memoria. Si no se necesitan los valores intermedios, y sólo se desea calcular el máximo común divisor de dos números enteros, conviene usar estas variantes:
Algoritmo de Euclides tradicional implementado de manera recurrente
Función mcd(a,b):
|
Algoritmo de Euclides tradicional implementado de manera iterativa
Función mcd(a,b):
|
Algoritmo de Euclides extendido implementado de manera recurrente
Función Euclides(a,b):
|
Algoritmo de Euclides extendido implementado de manera iterativa
Función Euclides(a,b):
|
Algoritmo de Euclides extendido implementado de manera iterativa con matrices
Función Euclides(a,b):
|
Acerca de la notación empleada:
 significa "asigne a la variable x el valor actual de y". En lenguajes como C, Java, C#, Python y Visual Basic esto significa simplemente
significa "asigne a la variable x el valor actual de y". En lenguajes como C, Java, C#, Python y Visual Basic esto significa simplemente x = y. En otros lenguajes como Pascal se traduce ena := b, en Maxima esa : b, en R, S y Ocaml esx <- y, e inclusive se utiliza la flechax ← ycomo el caso de APL. significa que primero se evalúan los valores a,b,c y luego se asigna
significa que primero se evalúan los valores a,b,c y luego se asigna  , etc. En lenguajes como Python, Ruby o Maxima esta instrucción tiene una estructura muy similar, como por ejemplo en Python:
, etc. En lenguajes como Python, Ruby o Maxima esta instrucción tiene una estructura muy similar, como por ejemplo en Python: (x,y,z) = (a,b,c). En otros lenguajes es necesario el uso de variables auxiliares, como por ejemplo en lenguaje C:aux1 = b; aux2 = c; x = a; y = aux1; z = aux2;.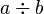 significa "el cociente de dividir a entre b". A esta operación se le conoce también como la división truncada porque trunca la parte fraccionaria del número. En muchos lenguajes de programación esto se implementa simplemente como
significa "el cociente de dividir a entre b". A esta operación se le conoce también como la división truncada porque trunca la parte fraccionaria del número. En muchos lenguajes de programación esto se implementa simplemente como a/b. Otras maneras sona\b(Visual Basic) ,a div b(Pascal) o biena//b(Python 3).- amod b significa "el residuo de dividir a entre b". A esta operación se le conoce simplemente como módulo. En muchos lenguajes de programación se implementa como
a % b, mientras que en otros esa mod b(Visual Basic o Pascal) o biena rem b(Ada).
Texto literal y prueba: http://latecladeescape.com/con-nombre-propio/algoritmo-de-euclides-mcd-y-mcm.html
Resumen: http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
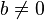 haga lo siguiente:
haga lo siguiente:








(0) Comments
Publicar un comentario